differentiate

Differentiate cfit or sfit object

Syntax

fx = differentiate(FO, X) [fx, fxx] = differentiate(...) [fx, fy] = differentiate(FO, X, Y) [fx, fy] = differentiate(FO, [x, y]) [fx, fy, fxx, fxy, fyy] = differentiate(FO, ...)

Description

For Curves

fx = differentiate(FO, X) differentiates the cfit object FO at the points specified by the vector X and returns the result in fx.

[fx, fxx] = differentiate(...) also returns the second derivative in fxx.

All return arguments are the same size and shape as X.

For Surfaces

[fx, fy] = differentiate(FO, X, Y) differentiates the surface FO at the points specified by X and Y and returns the result in fx and fy.

FO is a surface fit (sfit) object generated by the fit function.

X and Y must be double-precision arrays and the same size and shape as each other.

All return arguments are the same size and shape as X and Y.

If FO represents the surface $z = f (x, y)$ , then FX contains the derivatives with respect to x, that is, $\frac{d f}{d x}$ , and FY contains the derivatives with respect to y, that is, $\frac{d f}{d y}$ .

[fx, fy] = differentiate(FO, [x, y]), where X and Y are column vectors, allows you to specify the evaluation points as a single argument.

[fx, fy, fxx, fxy, fyy] = differentiate(FO, ...) computes the first and second derivatives of the surface fit object FO.

fxx contains the second derivatives with respect to x, that is, $\frac{\partial^{2} f}{\partial x^{2}}$ .

fxy contains the mixed second derivatives, that is, $\frac{\partial^{2} f}{\partial x \partial y}$ .

fyy contains the second derivatives with respect to y, that is, $\frac{\partial^{2} f}{\partial y^{2}}$ .

Examples

For Curves

Create a baseline sinusoidal signal:

xdata = (0:.1:2*pi)';
y0 = sin(xdata);

Add response-dependent Gaussian noise to the signal:

noise = 2*y0.*randn(size(y0)); 											
ydata = y0 + noise;

Fit the noisy data with a custom sinusoidal model:

f = fittype('a*sin(b*x)');
fit1 = fit(xdata,ydata,f,'StartPoint',[1 1]);

Find the derivatives of the fit at the predictors:

[d1,d2] = differentiate(fit1,xdata);

Plot the data, the fit, and the derivatives:

subplot(3,1,1)
plot(fit1,xdata,ydata) % cfit plot method
subplot(3,1,2)
plot(xdata,d1,'m') % double plot method
grid on
legend('1st derivative')
subplot(3,1,3)
plot(xdata,d2,'c') % double plot method
grid on
legend('2nd derivative')

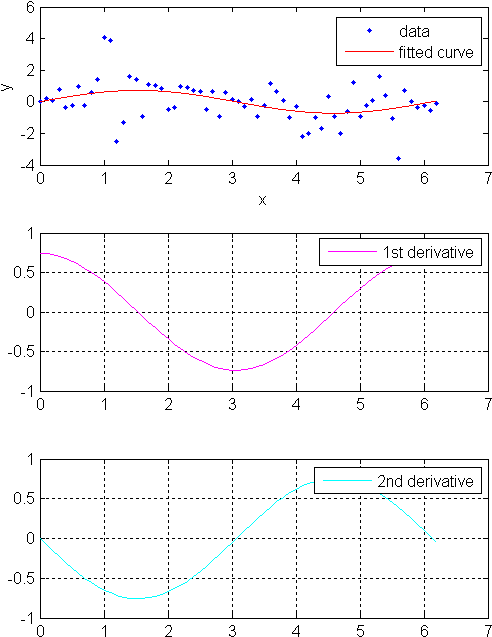
You can also compute and plot derivatives directly with the cfit plot method, as follows:

plot(fit1,xdata,ydata,{'fit','deriv1','deriv2'})

The plot method, however, does not return data on the derivatives, unlike the differentiate method.

For Surfaces

You can use the differentiate method to compute the gradients of a fit and then use the quiver function to plot these gradients as arrows. The following example plots the gradients over the top of a contour plot.

x = [0.64;0.95;0.21;0.71;0.24;0.12;0.61;0.45;0.46;...
0.66;0.77;0.35;0.66];
y = [0.42;0.84;0.83;0.26;0.61;0.58;0.54;0.87;0.26;...
0.32;0.12;0.94;0.65];
z = [0.49;0.051;0.27;0.59;0.35;0.41;0.3;0.084;0.6;...
0.58;0.37;0.19;0.19];
fo = fit( [x, y], z, 'poly32', 'normalize', 'on' );
[xx, yy] = meshgrid( 0:0.04:1, 0:0.05:1 );

[fx, fy] = differentiate( fo, xx, yy );

plot( fo, 'Style', 'Contour' );
hold on
h = quiver( xx, yy, fx, fy, 'r', 'LineWidth', 2 );
hold off
colormap( copper )

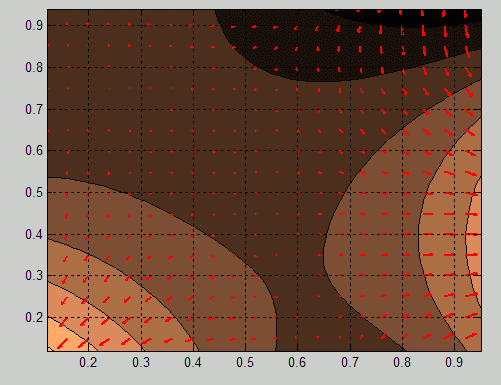
If you want to use derivatives in an optimization, you can, for example, implement an objective function for fmincon as follows.

function [z, g, H] = objectiveWithHessian( xy )
        % The input xy represents a single evaluation point
        z = f( xy );
        if nargout > 1
            [fx, fy, fxx, fxy, fyy] = differentiate( f, xy );
            g = [fx, fy];
            H = [fxx, fxy; fxy, fyy];
        end
    end

Tips

For library models with closed forms, the toolbox calculates derivatives analytically. For all other models, the toolbox calculates the first derivative using the centered difference quotient

$\frac{d f}{d x} = \frac{f (x + Δ x) - f (x - Δ x)}{2 Δ x}$

where x is the value at which the toolbox calculates the derivative, $Δ x$ is a small number (on the order of the cube root of eps), $f (x + Δ x)$ is fun evaluated at $x + Δ x$ , and $f (x - x Δ)$ is fun evaluated at $x - Δ x$ .

The toolbox calculates the second derivative using the expression

$\frac{d^{2} f}{d x^{2}} = \frac{f (x + Δ x) + f (x - Δ x) - 2 f (x)}{{(Δ x)}^{2}}$

The toolbox calculates the mixed derivative for surfaces using the expression

$\frac{\partial^{2} f}{\partial x \partial y} (x, y) = \frac{f (x + Δ x, y + Δ y) - f (x - Δ x, y + Δ y) - f (x + Δ x, y - Δ y) + f (x - Δ x, y - Δ y)}{4 Δ x Δ y}$

Documentation

differentiate

Syntax

Description

Examples

Tips

See Also

Introduced before R2006a

Curve Fitting Toolbox Documentation

Support