Interpolation Methods
About Interpolation Methods
Interpolation is a process for estimating values that lie between known data points.
Interpolant Methods
Method | Description |
|---|---|
Linear | Linear interpolation. This method fits a different linear polynomial between each pair of data points for curves, or between sets of three points for surfaces. |
Nearest neighbor | Nearest neighbor interpolation. This method sets the value of an interpolated point to the value of the nearest data point. Therefore, this method does not generate any new data points. |
Cubic spline | Cubic spline interpolation. This method fits a different cubic polynomial between each pair of data points for curves, or between sets of three points for surfaces. |
Shape-preserving | Piecewise cubic Hermite interpolation (PCHIP). This method preserves monotonicity and the shape of the data. For curves only. |
Biharmonic (v4) | MATLAB® 4 For surfaces only. |
Thin-plate spline | Thin-plate spline interpolation. This method fits smooth surfaces that also extrapolate well. For surfaces only. |
For surfaces, the Interpolant fit type uses the MATLAB scatteredInterpolant function
for linear and nearest methods, and the MATLAB griddata function for cubic and biharmonic
methods. The thin-plate spline method uses the tpaps function.
The type of interpolant to use depends on the characteristics of the data being fit, the required smoothness of the curve, speed considerations, post-fit analysis requirements, and so on. The linear and nearest neighbor methods are fast, but the resulting curves are not very smooth. The cubic spline and shape-preserving and v4 methods are slower, but the resulting curves are very smooth.
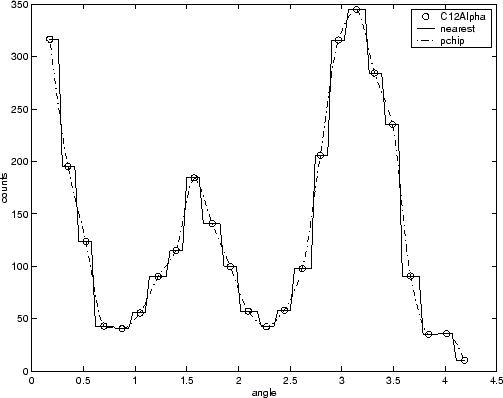
For example, the nuclear reaction data from the carbon12alpha.mat file
is shown here with a nearest neighbor interpolant fit and a shape-preserving
(PCHIP) interpolant fit. Clearly, the nearest neighbor interpolant
does not follow the data as well as the shape-preserving interpolant.
The difference between these two fits can be important if you are
interpolating. However, if you want to integrate the data to get a
sense of the total strength of the reaction, then both fits provide
nearly identical answers for reasonable integration bin widths.
Note
Goodness-of-fit statistics, prediction bounds, and weights are not defined for interpolants. Additionally, the fit residuals are always 0 (within computer precision) because interpolants pass through the data points.
Interpolants are defined as piecewise polynomials because
the fitted curve is constructed from many “pieces” (except
for Biharmonic for surfaces which is a
radial basis function interpolant). For cubic spline and PCHIP interpolation,
each piece is described by four coefficients, which the toolbox calculates
using a cubic (third-degree) polynomial.
Refer to the
splinefunction for more information about cubic spline interpolation.Refer to the
pchipfunction for more information about shape-preserving interpolation, and for a comparison of the two methods.Refer to the
scatteredInterpolant,griddata, andtpapsfunctions for more information about surface interpolation.
It is possible to fit a single “global” polynomial interpolant to data, with a degree one less than the number of data points. However, such a fit can have wildly erratic behavior between data points. In contrast, the piecewise polynomials described here always produce a well-behaved fit, so they are more flexible than parametric polynomials and can be effectively used for a wider range of data sets.