Surface Fitting to Biopharmaceutical Data
Curve Fitting Toolbox™ software provides some example data for an anesthesia drug interaction study. You can use Curve Fitting app to fit response surfaces to this data to analyze drug interaction effects. Response surface models provide a good method for understanding the pharmacodynamic interaction behavior of drug combinations.
This data is based on the results in this paper:
Kern SE, Xie G, White JL, Egan TD. Opioid-hypnotic synergy: A response surface analysis of propofol-remifentanil pharmacodynamic interaction in volunteers. Anesthesiology 2004; 100: 1373–81.
Anesthesia is typically at least a two-drug process, consisting of an opioid and a sedative hypnotic. This example uses Propofol and Reminfentanil as drug class prototypes. Their interaction is measured by four different measures of the analgesic and sedative response to the drug combination. Algometry, Tetany, Sedation, and Laryingoscopy comprise the four measures of surrogate drug effects at various concentration combinations of Propofol and Reminfentanil.
To interactively create response surfaces for this drug combination:
Use the Current Folder browser to locate and view the folder
matlab\toolbox\curvefit\curvefit.Right-click the file
OpioidHypnoticSynergy.txt, and select Import Data. The Import Wizard appears.Leave the default Column delimiters set to Tab and Column vectors in the Import tab.
Review the six variables selected for import: Propofol, Reminfentanil, Algometry, Tetany, Sedation, and Laryingoscopy.
On the Import tab, in the Import section, click Import Selection to import the dose-response data into the MATLAB® workspace.
Alternatively, you can import the data programmatically. Enter the following code to read the dose-response data from the file into the MATLAB workspace.
data = importdata( 'OpioidHypnoticSynergy.txt' ); Propofol = data.data(:,1); Remifentanil = data.data(:,2); Algometry = data.data(:,3); Tetany = data.data(:,4); Sedation = data.data(:,5); Laryingoscopy = data.data(:,6);
To create response surfaces you must select the two drugs for the X and Y inputs, and one of the four effects for the Z output. After you load the variables into your workspace, you can either open the tool and select variables interactively, or specify the initial fit variables with the
cftoolcommand.Enter the following to open Curve Fitting app (if necessary) and create a new response surface for
Algometry:cftool(Propofol, Remifentanil, Algometry)
Review the Curve Fitting app
X,Y, andZinput and output controls. The tool displays the selected variablesPropofol,RemifentanilandAlgometry, with a surface fit. The default fit is an interpolating surface that passes through the data points.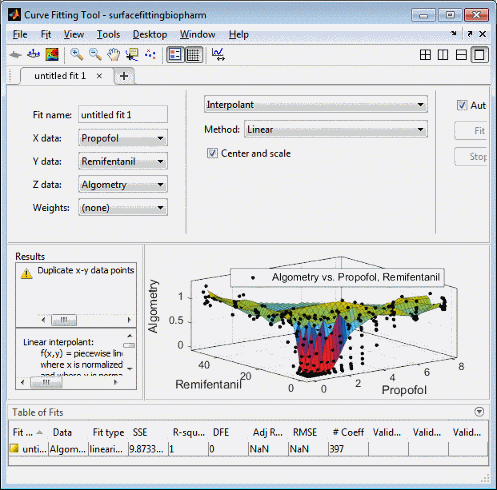
Create a copy of the current surface fit by either:
Selecting Fit > Duplicate
"Current Fit Name".Right-clicking a fit in the Table of Fits, and selecting Duplicate.
Select the Custom Equation fit type from the drop-down list to define your own equation to fit the data.
Select and delete the example custom equation text in the edit box.
You can use the custom equation edit box to enter MATLAB code to define your model. The equation that defines the model must depend on the input variables
xandyand a list of fixed parameters, estimable parameters, or both.The model from the paper is:
where CA and CB are the drug concentrations, and IC50A, IC50B, alpha, and n are the coefficients to be estimated.
You can define this in MATLAB code as
Effect = Emax*( CA/IC50A + CB/IC50B + alpha*( CA/IC50A )... .* ( CB/IC50B ) ).^n ./(( CA/IC50A + CB/IC50B + ... alpha*( CA/IC50A ) .* ( CB/IC50B ) ).^n + 1);Telling the tool which variables to fit and which parameters to estimate, requires rewriting the variable names
CAandCBtox, andy. You must includexandywhen you enter a custom equation in the edit box. AssumeEmax = 1because the effect output is normalized.Enter the following text in the custom equation edit box.
( x/IC50A + y/IC50B + alpha*( x/IC50A ) .* ( y/IC50B ) ).^n ./(( x/IC50A + y/IC50B + alpha*( x/IC50A ) .* ( y/IC50B ) ).^n + 1);
Curve Fitting app fits a surface to the data using the custom equation model.
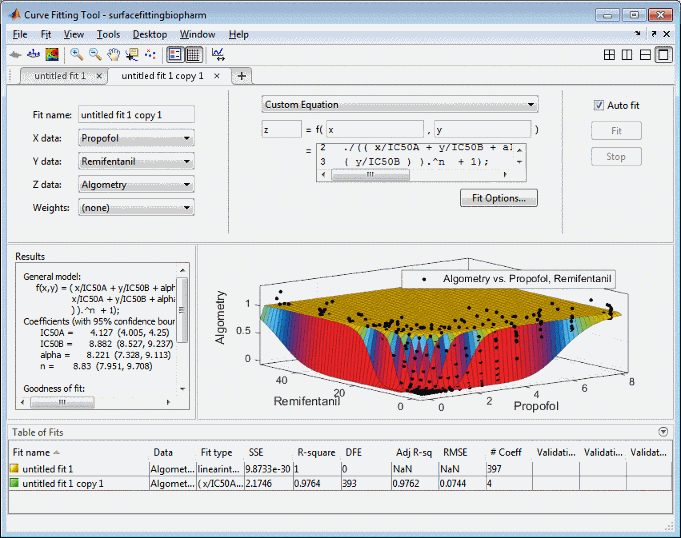
Set some of the fit options by clicking Fit Options under your custom equation.
In the Fit Options dialog box:
Set Robust to
LarSet the alpha StartPoint to 1 and lower bound to –5.
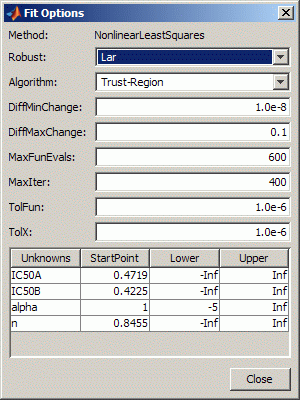
Leave the other defaults, and click Close.
The tool refits with your new options.
Review the Results pane. View (and, optionally, copy) any of these results:
The model equation
The values of the estimated coefficients
The goodness-of-fit statistics
Display the residuals plot to check the distribution of points relative to the surface by clicking the toolbar button
 or selecting View > Residuals Plot.
or selecting View > Residuals Plot.
To generate code for all fits and plots in your Curve Fitting app session, select File > Generate Code.
The Curve Fitting app generates code from your session and displays the file in the MATLAB Editor. The file includes all fits and plots in your current session.
Save the file with the default name,
createFits.m.You can recreate your fits and plots by calling the file from the command line (with your original data or new data as input arguments). In this case, your original data still appears in the workspace.
Highlight the first line of the file (excluding the word
function), and evaluate it by either right-clicking and selecting Evaluate Selection in Command Window, pressing F9, or copying and pasting the following to the command line:[fitresult, gof] = createFits(Propofol,... Remifentanil, Algometry)
The function creates a figure window for each fit you had in your session. The custom fit figure shows both the surface and residuals plots that you created interactively in the Curve Fitting app.
Create a new fit to the Tetany response instead of Algometry by entering:
[fitresult, gof] = createFits(Propofol,... Remifentanil, Tetany)
You need to edit the file if you want the new response label on the plots. You can use the generated code as a starting point to change the surface fits and plots to fit your needs. For a list of methods you can use, see
sfit.
To see how to programmatically fit surfaces to the same example problem, see Surface Fitting With Custom Equations to Biopharmaceutical Data.